Inhaltsverzeichnis
Sinus
sinus cosinus integer numbers
Das Beispiel ist in gforth codiert worden.
Erklärung
Um den Sinus eines Winkels mit ganzen Zahlen (integer) darstellen zu können, skaliert man passend zur Anwendung. Benötigt man z.B. vier Stellen des Sinuswertes, wird er mit 10K multipliziert ausgegeben.
In einem Mikrokontroller geht es bei so einer Funktion auch um eine Balance zwischen Speicherplatz und Rechenzeit. So hat es sich eingebürgert Stützwerte für den Sinus aus einer Tabelle zu entnehmen, und lediglich bei Bedarf Zwischenwerte zu berechnen. Als Index in so eine Tabelle eignet sich die Gradzahl besser als das Bogenmaß. Um die Tabelle klein zu halten, werden oft nur die Sinuswerte von 0 - 90 Grad abgelegt - also die erste Viertelwelle. Manchmal werden auch nur 45 Werte in 2-Grad-Schritten abgelegt.
Um nun alle ganzen Zahlen als Winkel verwenden zu können, muss ein gegebener Winkel auf diese ersten 90 Grad zurück geführt werden. Weil der Sinus eine periodische Funktion ist, können alle Gradzahlen durch entsprechende Phasenverschiebung einfach auf die erste Viertelwelle zurück geführt werden. Es muss dabei jedoch eine Korrektur für das Vorzeichen des Sinuswertes erfolgen.
Baut man den Algorithmus um den Tabellenzugriff
cell * sinustabelle + @
auf, erhält man folgenden Ablauf. Winkel zwischen 90 und 180 Grad werden in den ersten Quadranten gespiegelt.
180 swap - ( 90..180Grad — 0..90Grad )
Winkel zwischen 180 und 360 Grad werden eine Halbwelle tiefer geschoben.
180 - ( 180..360Grad — 0..180Grad )
Weil dabei das Vorzeichen wechselt, wird ein flag hinterlegt, mit dem zum Schluß das Vorzeichen angepasst wird.
true >r … r> IF negate THEN
Winkel größer als 360 Grad werden auf die erste Welle abgebildet.
360 mod
Und negative Gradzahlen werden in den positiven Bereich umgeklappt. Auch dabei wechselt das Vorzeichen, und ein weiteres Flag wird hinterlegt, mit dem das Vorzeichen umgekehrt werden kann.
dup 0< >r abs … r> IF negate THEN
Algorithmus
\ Sinus und Cosinus
\ Tabellengestützte Berechnung für ganze Zahlen.
\ Ergibt auf 10K skalierte Werte.
\ Prototypische Lösung mittels:
\ Gforth 0.6.2, Copyright (C) 1995-2003 Free Software Foundation, Inc.
vocabulary sinus sinus definitions decimal
create sinustabelle \ 0...90 Grad, Index in Grad
0000 , 0175 , 0349 , 0523 , 0698 , 0872 ,
1045 , 1219 , 1392 , 1564 , 1736 , 1908 ,
2079 , 2250 , 2419 , 2588 , 2756 , 2924 ,
3090 , 3256 , 3420 , 3584 , 3746 , 3907 ,
4067 , 4226 , 4384 , 4540 , 4695 , 4848 ,
5000 , 5150 , 5299 , 5446 , 5592 , 5736 ,
5878 , 6018 , 6157 , 6293 , 6428 , 6561 ,
6691 , 6820 , 6947 , 7071 , 7193 , 7314 ,
7431 , 7547 , 7660 , 7771 , 7880 , 7986 ,
8090 , 8192 , 8290 , 8387 , 8480 , 8572 ,
8660 , 8746 , 8829 , 8910 , 8988 , 9063 ,
9135 , 9205 , 9272 , 9336 , 9397 , 9455 ,
9511 , 9563 , 9613 , 9659 , 9703 , 9744 ,
9781 , 9816 , 9848 , 9877 , 9903 , 9925 ,
9945 , 9962 , 9976 , 9986 , 9994 , 9998 ,
10000 ,
: sinus@ cell * sinustabelle + @ ;
: sin ( grad -- sinus )
dup 0< >r abs
360 mod
dup 180 > if 180 - true >r else false >r then
dup 90 > if 180 swap - then
sinus@
r> if negate then
r> if negate then ;
: cos 90 + sin ;
( finis)
Verifikation
Da gforth die Funktion fsin bietet, kann ein Vergleich der Tabelleneinträge mit dem berechneten Wert durchgeführt werden. Jedem sin aus der Tabelle wird ein fsin gegenübergestellt.
fsin nimmt ein Bogenmaß in Fließkomma Darstellung, daher muss die Gradzahl dahin umgerechnet werden.
\ Verifikation : .sin sin 6 .r space ; ( rad = grad * pi / 180 ) : rad d>f pi f* 180.0e0 f/ ; : .fsin s>d rad fsin 10e3 f* 14 6 4 f.rdp ; : test ( von bis -- ) swap DO cr i .sin i .fsin LOOP ;
Als Ergebnis erhalten wir:
Gforth 0.6.2, Copyright (C) 1995-2003 Free Software Foundation, Inc.
Gforth comes with ABSOLUTELY NO WARRANTY; for details type `license'
Type `bye' to exit
0 91 tt
0 0.000000
175 174.524064
349 348.994967
523 523.359562
698 697.564737
872 871.557427
1045 1045.284633
1219 1218.693434
1392 1391.731010
1564 1564.344650
1736 1736.481777
1908 1908.089954
2079 2079.116908
2250 2249.510543
2419 2419.218956
2588 2588.190451
2756 2756.373558
2924 2923.717047
3090 3090.169944
3256 3255.681545
3420 3420.201433
3584 3583.679495
3746 3746.065934
3907 3907.311285
4067 4067.366431
4226 4226.182617
4384 4383.711468
4540 4539.904997
4695 4694.715628
4848 4848.096202
5000 5000.000000
5150 5150.380749
5299 5299.192642
5446 5446.390350
5592 5591.929035
5736 5735.764364
5878 5877.852523
6018 6018.150232
6157 6156.614753
6293 6293.203910
6428 6427.876097
6561 6560.590290
6691 6691.306064
6820 6819.983601
6947 6946.583705
7071 7071.067812
7193 7193.398003
7314 7313.537016
7431 7431.448255
7547 7547.095802
7660 7660.444431
7771 7771.459615
7880 7880.107536
7986 7986.355100
8090 8090.169944
8192 8191.520443
8290 8290.375726
8387 8386.705679
8480 8480.480962
8572 8571.673007
8660 8660.254038
8746 8746.197071
8829 8829.475929
8910 8910.065242
8988 8987.940463
9063 9063.077870
9135 9135.454576
9205 9205.048535
9272 9271.838546
9336 9335.804265
9397 9396.926208
9455 9455.185756
9511 9510.565163
9563 9563.047560
9613 9612.616959
9659 9659.258263
9703 9702.957263
9744 9743.700648
9781 9781.476007
9816 9816.271834
9848 9848.077530
9877 9876.883406
9903 9902.680687
9925 9925.461516
9945 9945.218954
9962 9961.946981
9976 9975.640503
9986 9986.295348
9994 9993.908270
9998 9998.476952
10000 10000.000000 ok
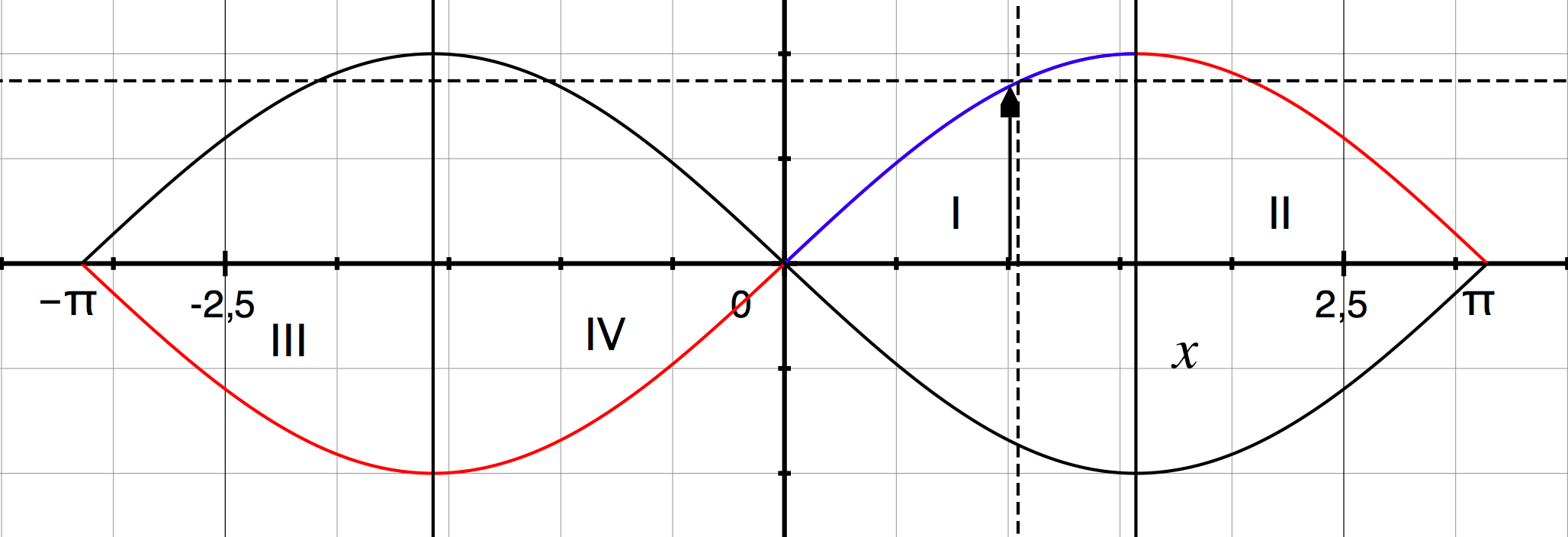
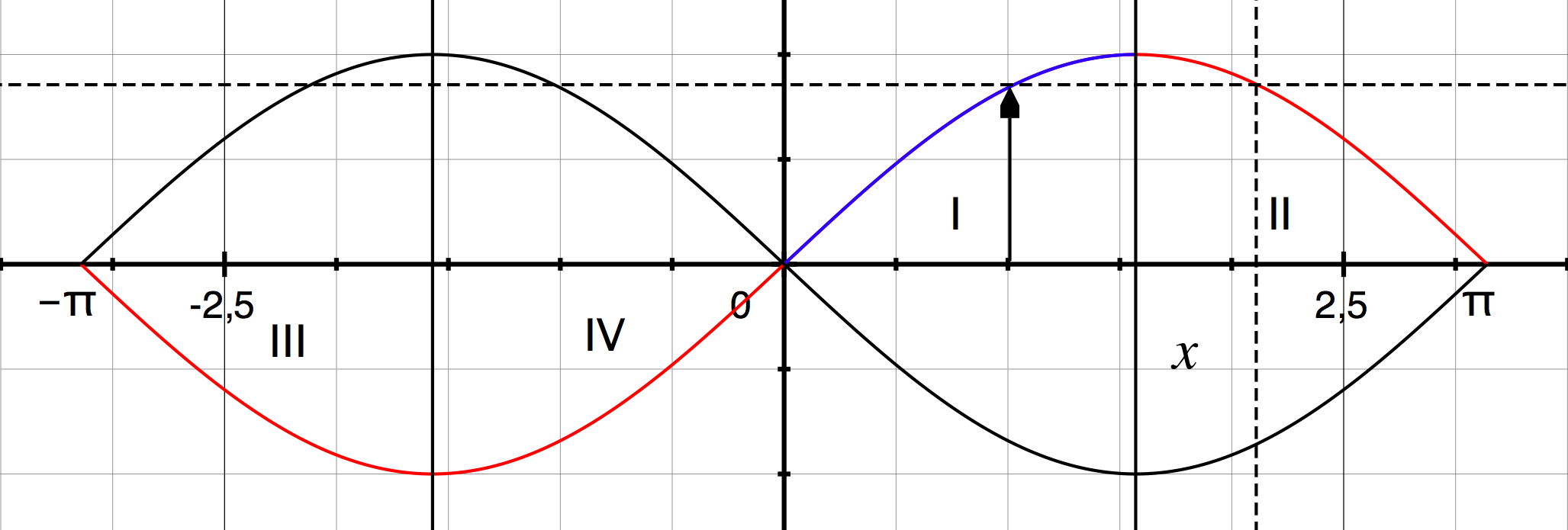
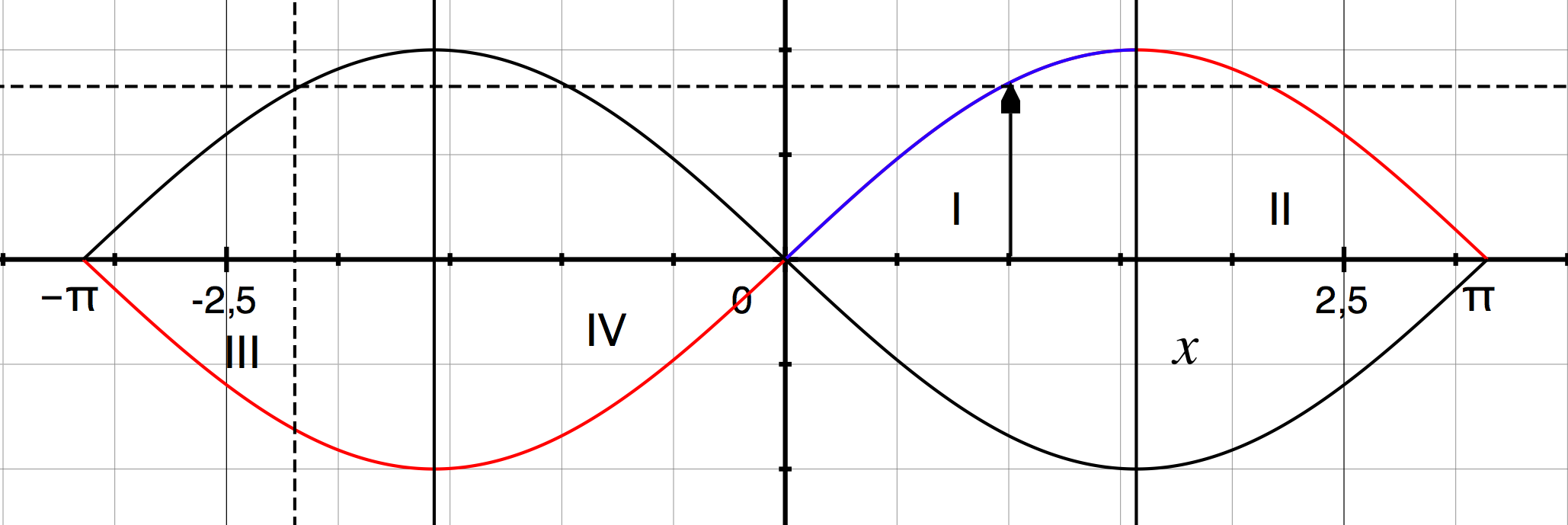
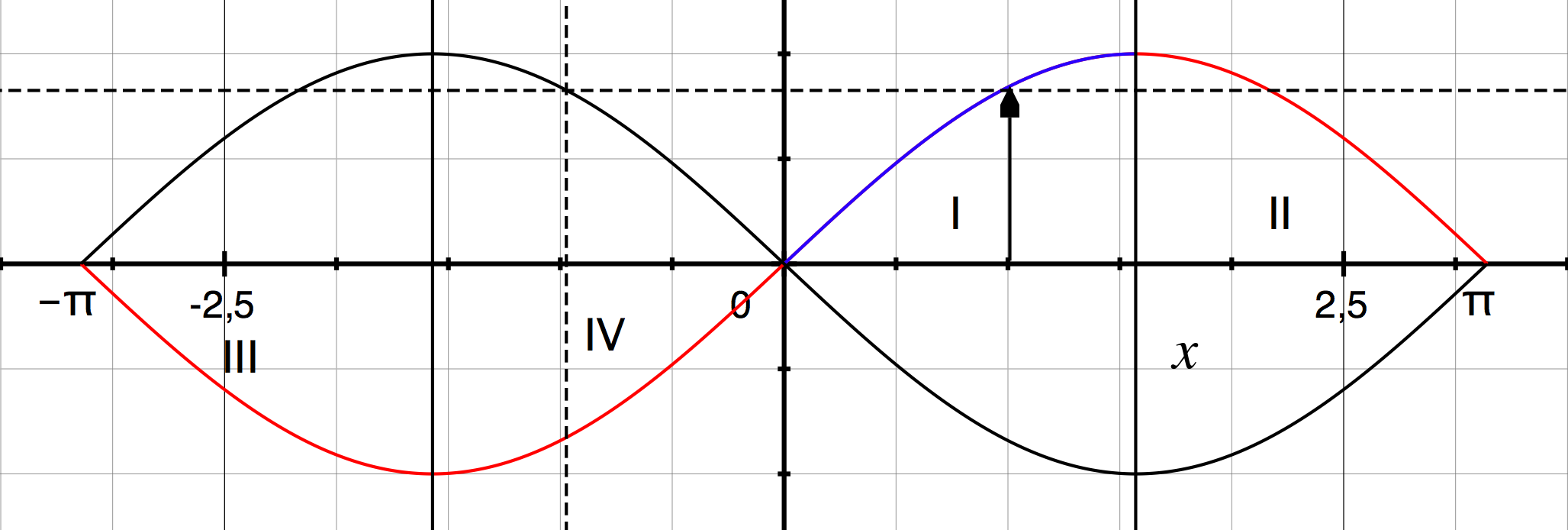
Grafische Darstellung
Quellen bzw Links
Sinusberechnung als lineare Interpolation
Im vorliegenden Fall kann davon ausgegangen werden, dass die Datenbereiche von x und y begrenzt sind. Man kann sich die Aufnahme der Sinusfunktion so vorstellen, dass eine Leiste der Länge L im Quadranten zwischen x- und y-Achse bewegt wird. In diesem Fall hat x den Wertebereich zwischen 0 (Leiste auf x-Achse) und dem rechten Winkel(Leiste auf y-Achse). y hat dann den Wertebereich zwischen 0 und L. In diesem Bereich gibt es fünf rationale Wertepaare:
(0;0),(1/3;1/2),(1/2;0,707);(2/3;0,866),(1;1), was den Werten für 0, 30, 45, 60 und 90 Grad entspricht.
Die Idee war es nun, die beiden Werte auf den Zahlenbereich von 32767 zu skalieren. Außerdem wurden noch zwei Stützwerte ergänzt, für 15 und 75 Grad.
variable sinus
5461 , \ Einteilung (= 32767/6 <=> 90° /6 )
0 , 8191 , 16383 , 23166 , 28376 , 31718 , 32767 , \ Werte
: schrittweite sinus 2 + @ ;
: stuetzwert ( wertnr --- wert ) 2 * 4 + sinus + @ ;
:sin (winkel --- wert ) schrittweite /mod
dup rot swap dup
stuetzwert swap 1 + stuetzwert swap -
schrittweite */
swap stuetzwert + ;
Man muß den Winkel entspechend mit „*/“ skalieren und anschließend auch das Ergebnis.
Die Funktion bietet sich auch bei Anwendungen an, wo nur Stützwerte bekann sind, z.B. bei der Leuchtenberechnung.